Comprendre l'analyse modale

La résolution numérique de problèmes dynamiques suivant une approche linéaire (la notion de dynamique linéaire sera traitée dans un autre article) nécessite en préambule une analyse modale. Le terme analyse modale s'accompagne souvent des termes fréquences propres et modes propres. Le mot propre y a toute son importance car il souligne la singularité du comportement du système étudié.
Quelle définition donner à l'analyse modale ?
L'analyse modale met en évidente les différents modes de déformations générées par des vibrations que pourrait adopter un système mécanique en réponse à une sollicitation. Elle peut être vue comme la recherche des réponses élémentaires d'un système (une structure par exemple) si cette dernière venait à être excitée .
La réponse du système à une excitation est dite globale. Le terme réponse élémentaire signifie que si la réponse globale venait à être décomposée, elle serait la superposition de plusieurs réponses élémentaires.

Notions de fréquences propres et modes propres
C'est peut paraitre évident mais il convient de le souligner pour bien comprendre la suite. Une sollicitation identique imposée à plusieurs systèmes différents ne produira pas les mêmes effets. Pourquoi ?
Parce que chaque système réagira différemment en fonctions de ses propres caractéristiques.
Les fréquences propres sont une représentation de ces caractéristiques. Aussi appelées fréquences naturelles, elles correspondent aux fréquences de vibrations du système où sa réponse est maximale. On parle aussi de fréquences de résonance. Elles ne dépendent que de la masse du système et de sa rigidité (propriétés matériaux, géométriques, …).
A chacune des fréquences propres correspond un mode propre qui est la représentation du déplacement de la matière du fait de la sollicitation imposée.


Masse effective participative et facteur de participation
Lorsqu'un système mécanique est sollicité, chacun de ses modes propres fait participer une fraction de sa masse totale qui est variable selon les directions du système de coordonnées considéré. C'est ce qu'on appelle la masse effective modale ou la masse effective participative (EMPF : Effective Mass participation Factor)
Certains modes sont dominants car ils font participer une part de masse plus importante que les autres modes dans une direction donnée.
Pour avoir une réponse globale représentative de l'excitation imposée au
système, il est recommandé que le cumul des masses effectives participatives (CEMPF : Cumulative Effective Mass Participation Factor) extraites dans chaque direction correspondent au moins à 90% de la masse totale du système.
Le facteur de participation en masse (Mass Participation Factor) est une autre lecture de participation des masses effectives modales. Elle révèle le niveau de contribution en masse d'un mode.
La relation entre la masse effective modale et le facteur de participation en masse est s'exprime comme suit :
Où pour une direction donnée :
m_ {\footnotesize mode \, i} ^{\footnotesize effective} \text{: masse effective participative du mode propre i}
\Gamma_{\footnotesize mode \, i} \text{: Facteur de participation en masse du mode propre i}
m_{\footnotesize mode \, i} ^{\footnotesize generalized} \text{: masse généralisée du mode propre i}
A présent, illustrons ces notions dans un cas d'application
Soit une plaque mince d'acier ABCD encastrée à une de ses extrémités. Le système de coordonnées XYZ est tel que (AD) est parallèle à (OY) et (AB) parallèle à (OX).
L'objectif de cette étude est de déterminer les fréquences et les modes propres du système ainsi que les modes les plus impactants.

Longueur de la plaque L = 1000mm
Largeur de la plaque d = 400mm
Epaisseur de la plaque t = 5mm
Matériau : acier
Densité : 7.8 E-9 tonne /mm3
Module de Young E = 210 000 MPa
Coefficient de poisson : 0.3
Extraction des modes propres
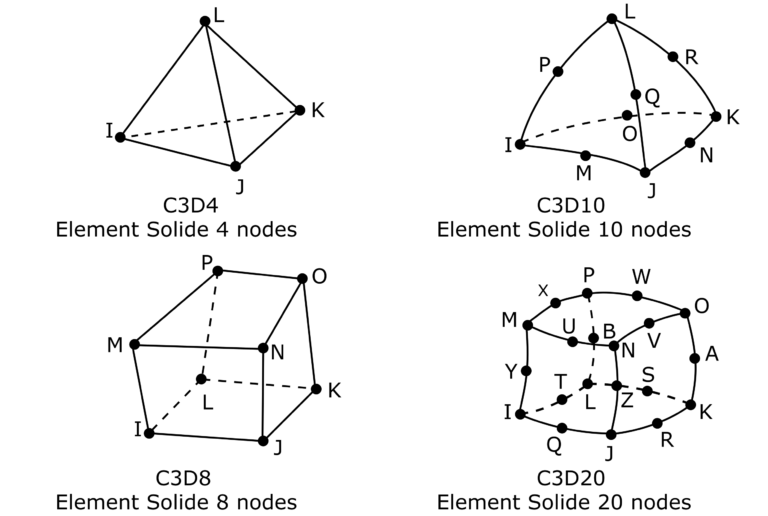
De nombreux solveurs éléments finis permettent d'extraire les fréquences propres et les modes propres d'un système. Nous allons utiliser ABAQUS qui est la solution élément finis dont nous disposons chez SIMUMECA.
Pour réaliser une analyse modale, aucun chargement n'est requis, seules les conditions limites sont à définir. Dans notre cas, l'extrémité AD sera encastrée.
Dans les paramètres d'ABAQUS, on définit :
- La méthode à utiliser (LANCZOS, SUBSPACE ou AMS). On prendra Lanczos
- Le nombre de modes à extraire ou une plage de fréquences dans laquelle tous les modes possibles seront extraits.





Résultats de l'analyse
5 modes propres ont été extraits avec leurs fréquences et valeurs propres associées. Ces résultats sont présentés dans le fichier .DAT généré par le calcul ABAQUS.

Vérification de la participation des masses
Les masses effectives participatives des mouvements de translation ont été analysées pour les 5 modes extraits.
Le 1er mode fait participer 61% de la masse globale du système dans la translation suivant la direction Z. Il s'agit du mode dominant. Le mode 3 et le mode 5 suivent avec des masses effectives participatives de 19% et 7% respectivement.
Les directions X et Y ne font pas participer de masse. Le déplacement de la matière se
fait uniquement selon Z.
Représentativité du comportement global
Le cumul des masses effectives participatives est proche de 90% dans la direction Z mais nul dans les directions X et Y. Avec les 5 modes extraits, nous avons donc une assez bonne représentation du comportement du système selon la direction Z, mais pas d'informations sur le comportement dans les autres directions.
Qu'en serait-il avec beaucoup plus de modes propres extrait ?
Poussons l'extraction jusqu'à 20 modes pour voir
Avec 20 modes extraits, on remarque que le cumul des masses effectives participatives en Z passe de 87% à 94%.
Le mode 13 est le plus impactant selon la direction Y. En effet, sa masse effective modale dans cette direction vaut 62% de la masse totale du système.
Sur les 20 modes extraits, la direction X ne fait participer aucune masse. Ce qui veut dire les modes extraits sont insuffisants pour couvrir le comportement de la plaque notamment suivant la direction X.

Facteur de participation en masse
Pour information,
Les masses participatives des mouvements de translation ont été analysées pour les 5 modes

Importance du centre de masse dans la réponse modale
Il est possible d'avoir des modes propres où la déformée selon une direction est non nulle, ce qui suggérerait alors que sa masse effective modale dans cette même direction soit non-nulle; ce qui n'est pas le cas !
L'explication vient du fait que le calcul des modes propres indique comment le centre de masse du système réagit à l'excitation. Vous observerez que dans ce cas de figure, le centre de masse reste fixe alors que d'autres parties sont déformées.
Conditions limites et cumul des masses effectives modales
Les masses dans les zones de conditions limites où les mouvements sont restreints ne peuvent participer à la réponse du système
Bibliographie
1. Abaqus Theory Manual
2. L. Champaney & al. Exemples de vibrations des plaque avec des défauts