Introduction
Le développement des équipements submersibles est soumis à une phase de test pour valider leur utilisation en toute sécurité dans les conditions réelles, c’est-à-dire en mer profonde. Pour réaliser ces tests, on utilise des systèmes de simulation de conditions en mer profonde. Il s'agit d'un moyen idéal pour valider l'utilisation en toute sécurité des équipements submersibles et de vérifier la tenue mécanique et la fiabilité de l'équipement sous pression. Les simulateurs de conditions de mer profondeur sont constitués d'une chambre de pression dont l'étanchéité est un sujet majeur en raison des grandes tailles des joints, des surfaces d'étanchéité et des importantes pressions exercées. Dans ce post, nous traiterons de la simulation d'un joint torique pour ce type d'application, d'une approche de validation des performances des joints toriques de grandes tailles en utilisant les méthodes numériques par éléments finis.
A propos des joints toriques
Les joints toriques dans les applications en mer profonde
Les joints d'étanchéité des chambres de pression en eau profonde sont de type statique, c’est-à-dire qu'il n' y a pas de mouvement relatifs entre le joint les surfaces d'appuis lorsque le système est en fonctionnement (voir article), contrairement par exemple à un système seringue où l'étanchéité est dynamique. Les joints en élastomère de forme torique sont les plus couramment utilisés pour les applications de chambres sous pression et ce sont aussi les plus répandus de manière générale dans l'industrie. En effet, ils présentent l'avantage de disposer d'un design simple, d'être légers et facile à remplacer lorsqu'ils vieillissent ou se détériorent.

Illustration des joints toriques
Dimensionner un joint torique
Plusieurs paramètres sont à prendre en compte dans le dimensionnement d'un joint torique. Nous les classerons en 5 principales catégories
1) Le design du joint et de emplacement : Le joint torique est caractérisé par son diamètre intérieur (ID) et sa section transversale (CS). Par ailleurs, il existe différentes formes géométriques destinées à accueillir le joint. Leur design a une incidence sur la performance du joint.
2) Le matériau : Plusieurs élastomères sont utilisés pour les joints toriques (NBR, PTFE, EPR, CSM, ...) . La performance des joints toriques ainsi que leur durée de vie dépendront d'eux. L'un des plus utilisés étant le NBR (Nitrile Butadiene Rubber).
3) Le jeu d'étanchéité : Il est directement lié à la contrainte initiale de compression du joint et intervient directement dans le mécanisme d'auto-étanchéité (voir article).
Plus le jeu d'étanchéité est réduit, plus la contrainte initiale de compression sera élevée; et plus le joint sera étanche.
4) La pression du fluide : Dans un joint torique, l'étanchéité se fait lorsque le système est mis sous pression. On parle alors de mécanisme d'auto-étanchéité. Il se traduit par l'équation représentée en Fig. 1 (Sigma_P = Sigma_0 + P)
5) Le coefficient de friction : Il dépend de la rugosité des surfaces en jeu. De manière générale, il est pris égal à 0.5 pour un contact sans lubrification acier/élastomère.
Des simulations ont démontré que c'est le paramètre le moins impactant parmi ceux pré-cités.

B. Modélisation par éléments finis d'un joint torique
Etude de la performance d'un joint torique de grande dimension pour des applications à très hautes pressions (simulateur de conditions de pression en fond marin).
1) Description du système :
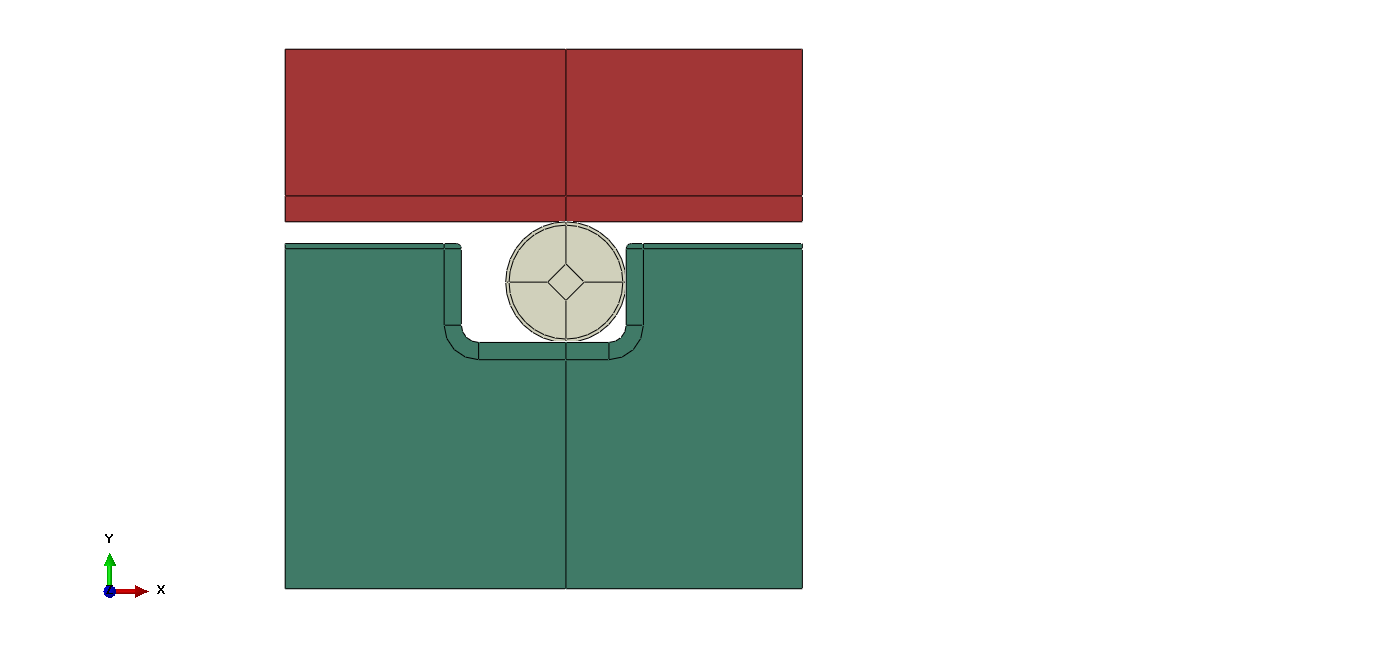
2) Matériau :
Les parties fixe et mobile sont en acier inoxydable AISI 316L tandis que le joint torique est en NBR (Nitrite Butdiene Rubber).
L'acier est modélisé par une loi élastique linéaire de type Hook tandis que l'élastomère est modélisé par une loi de comportement de type Polynomiale (Mooney Rivlin étant la forme polynomiale lorsque N =2).


4) Approche de modélisation et étapes de calcul :
La modélisation par éléments finis se fera selon une approche directe couplée thermomécanique. Le solveur Abaqus Explicit sera utilisé. Le calcul comportera deux étapes. La première, durant laquelle le disque sera en rotation libre pour simuler la vitesse stationnaire atteinte par le cycliste. La deuxième sera celle du freinage.
5) Conditions limites :
La partie fixe sera encastrée à sa base, tandis que la partie mobile se déplacera à une vitesse constante jusqu'à l'obtention du jeu d'étanchéité souhaité.
La pression marine maximale dans les fonds marins atteint 115 MPa. Pour le dimensionnement du joint torique, une marge de sécurité de 50% est considérée, ce qui conduit à pression maximale du fluide de 200 MPa.
L'impact de ces 2 paramètres (pression du fluide et jeu d'étanchéité) sera évalué à travers un plan d'expérience numérique. Plusieurs cas seront simulés en faisant varier la pression du fluide entre 10 MPa et 200 MPa par incrément de 10 MPa, tandis que le jeu d'étanchéité variera de 0 mm à 0.5 mm par incrément de 0.1 mm.
C. Résultats de la simulation numérique
Etude de la performance d'un joint torique de grande dimension pour des applications à très hautes pressions (simulateur de conditions de pression en fond marin).
1) Critère de contraintes :
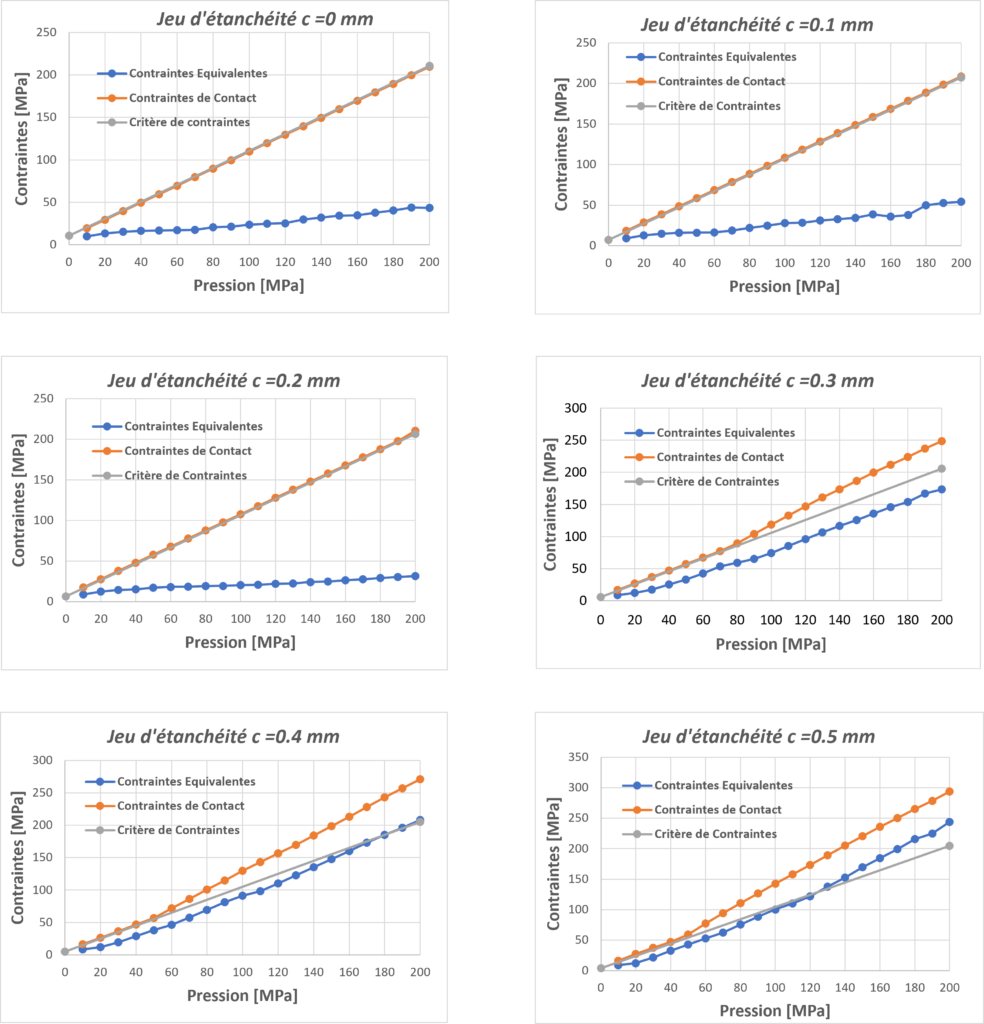
Ci-dessous quelques résultats montrant le profil des contraintes de contact avec un jeu d'étanchéité et une pression de fluide.



Le critère de contraintes suggère que la contrainte de contact sigma_P évolue linéairement en fonction de la pression du fluide P. Lorsque cette relation n'est pas respectée, on peut considérer que la situation représente un danger ou un défaut de conception.
Les relevés de contraintes de contact ci-dessous montrent que le critère de contraintes est respecté sur toute la plage de pression pour les jeux d'étanchéité c=0.1mm et c=0.2mm.
Pour c=0.3 mm, la pression maximale du fluide est de 80 MPa. Au delà, la relation linéaire n'est plus respectée. Pour c=0.5mm, la pression maximale admissible du fluide est 50 MPa.
2) Critère de déformations :
Le critère de déformation utilisé ici est basé sur les travaux de JT. Baumann qui dans son ouvrage " Fatigue, Stress, and Strain of Rubber Components. A Guide for Design Engineers" a établi que les joints toriques sont performants tant que les déformations sont inférieures à 100%.
Avec la marge de sécurité de 1.5 introduite plus tôt, le taux de déformations maximales admissibles est réévalué à 67 %.
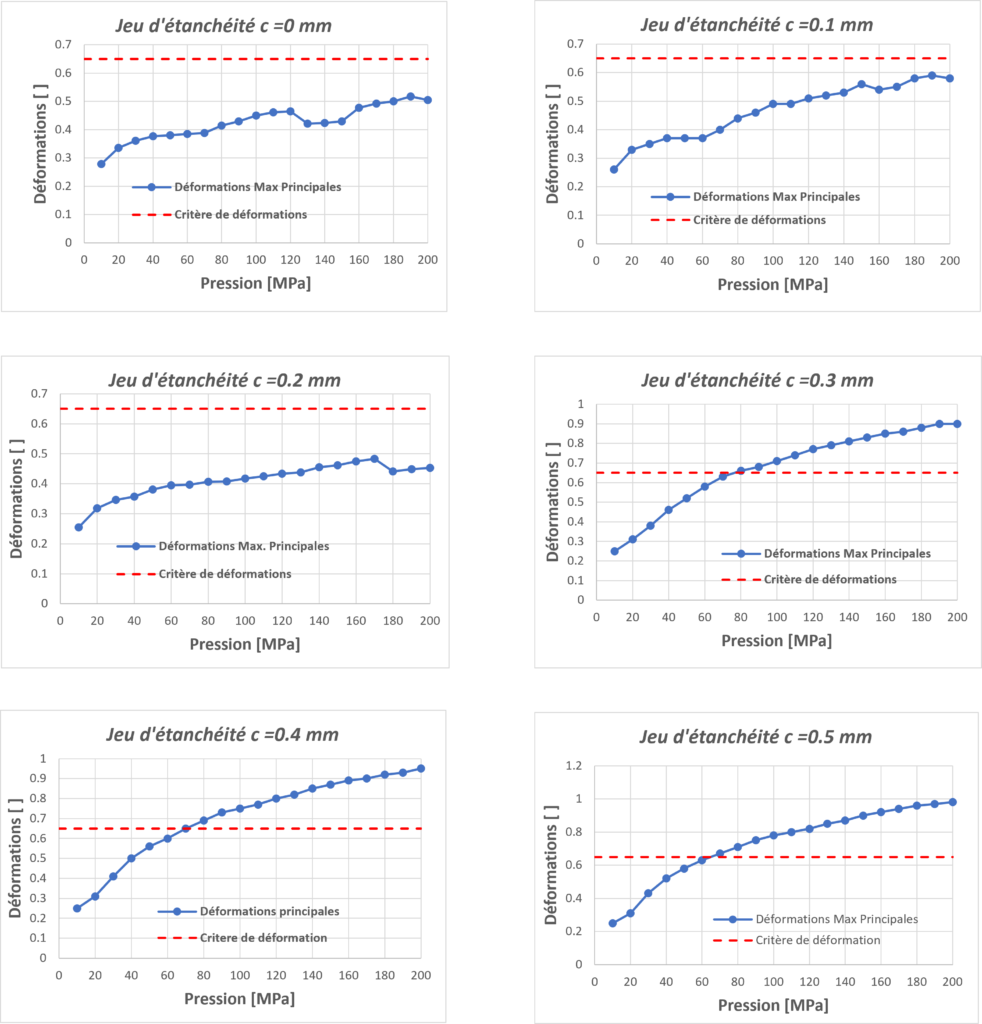
Ci-dessous une vue des déformations maximales principales dans les situations étudiées.



Le critère de déformation prédit des résultats similaires au critère de contraintes.
Lorsque le jeu d'étanchéité est nul, les déformations maximales sont inférieures à 67%, validant la performance du joint torique jusqu'à 200 MPa. Ce qui est aussi valable pour c=0.2mm. Lorsque c=0.3mm, la pression maximale admissible est de 70 MPa. .
Pour les valeurs de jeu d'étanchéité de 0.4mm 0.5mm, les critères de contraintes et de déformations présentent un léger écart dans la prédiction des performances des joints toriques. Pour garantir la sécurité des équipements et des personnes, on retiendra toujours le critère le plus conservatif des deux.
D. Conclusion de l'étude
L'analyse des performances d'un joint torique a été réalisée par la méthode de simulation numérique par éléments finis avec le solveur ABAQUS / Standard.
Les résultats obtenus démontrent que le jeu d'étanchéité et la pression du fluide jouent un rôle fondamental dans le mécanisme d'étanchéité.
- La pression de contact du joint torique avec les surfaces à étanchéifier évolue linéairement avec la pression du fluide, ce qui démontre du bon état du joint.
- Plus on réduit le jeu d'étanchéité, plus on augmente la performance du joint torique. Toutefois, la réduction de ce jeu n'est pas toujours évidente en raison de certaines contraintes liées à la conception de l'équipement.
Bibliographie
1. Wentao Song & al - Finite element analysis of large-sized O-rings used in deep-ocean pressure chambers
2. JT Bauman - Fatigue, Stress, and Strain of Rubber Components : a guide for design engineers