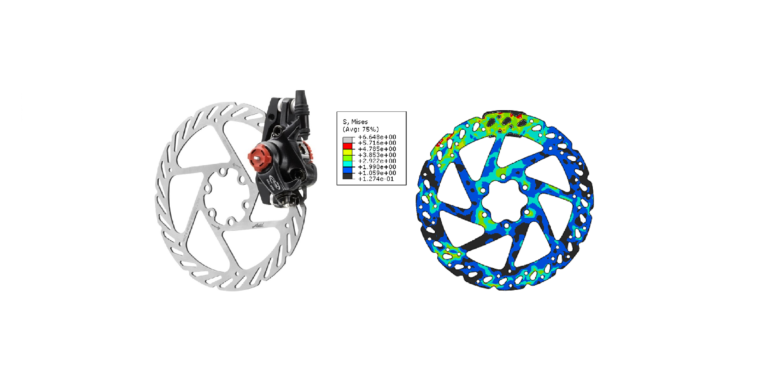
Nous entamons une série d'articles consacrés aux éléments finis au cours desquels seront abordés les différents types d'éléments finis, leurs caractéristiques et les conditions dans lesquelles il est recommandé de les utiliser.
Nous allons présenter dans cet articles les principaux points à prendre en compte lors de la sélection du type d'éléments finis lorsqu'on modélise un problème.
Introduction
ABAQUS dispose d'un large panel d'éléments pour résoudre les problèmes physiques par la méthode des éléments finis.
Pour construire un modèle pertinent afin d'apporter la solution la plus précise, le bon choix d'éléments finis est indispensable.
Nous allons présenter dans cet articles les principaux points à prendre en compte lors de la sélection du type d'éléments finis lorsqu'on modélise un problème.
Elements finis : définition simplifiée et caractéristiques
La méthode des éléments finis consiste à découper en plusieurs très petites fractions le domaine de l'étude (géométrie de pièces, assemblages, ...) afin d'y résoudre des équations fondamentales de la physique associé à la problématique (statique, dynamique, thermique, ...). Cette résolution nécessite l'application des conditions limites (de frontières)que nous n'aborderons pas dans cet article.
L'opération consistant à subdiviser le domaine d'étude s'appelle le maillage ("meshing" en anglais). On peut la décrire comme une discrétisation spatiale.
Les éléments finis peuvent être classés selon 5 caractéristiques que nous détaillons ci-dessous

Illustration d'un maillage
Les familles d'éléments finis
Elles sont essentiellement associées au type de géométrie que l'on souhaite modéliser. Les éléments beams sont adaptés aux représentations 1D des éléments poutres. Les éléments shell (2D) sont surfaciques, ils permettent de modéliser des pièces et assemblages à parois fines. L'épaisseur est dans ce cas une donnée numérique. Les éléments connecteurs eux, permettent de modéliser divers liaisons cinématiques, des ressorts ou amortisseurs. Les éléments solides (3D) quant à eux, sont associés à une représentation volumique et permettent de tout modéliser avec beaucoup plus de détails. Ils nécessitent aussi beaucoup plus de temps de modélisation et de calcul. Les éléments infinis trouvent par exemple leur application dans l'acoustique pour éviter la réflexion d'ondes.

Famille d'éléments finis dans ABAQUS
Les degrés de liberté (DDL) des nœuds
Ils sont associés à un nœud et représentent selon le domaine physique étudié les déplacements, températures, pression acoustiques, …Ils sont aussi dépendants des familles d'éléments évoqués plus haut.
En effet, dans une analyse de type structurelle (contraintes - déplacements), les éléments solides (3D) ont 3 DLL, tous en translations tandis que les éléments shell ont 6 DDL : 3 rotations + 3 translations.
Dans une analyse de type thermique (heat transfer), chaque nœud a un seul degré de liberté par dimension correspond à la température (1DDL pour les éléments 1D, 2DDL pour les éléments 2D et 3DDL pour les éléments 3D). Pour une analyse en couplage fort thermo-mécanique, chaque nœud dispose des DDL de l'analyse mécanique (structurelle) en plus de ceux pour l'analyse thermique.
Exemple : 1 nœud d'un élément solide (3D) disposera de 6 DDL au total (3 DDL pour la partie mécanique + 3 DDL pour la partie thermique ).
Nombres de nœuds des éléments
Un élément fini est constitué de plusieurs nœuds. Leur nombre varie en fonction de la famille d'éléments et leur ordre. Le nombre de nœuds au sein d'un élément est donc directement lié à son degré de liberté qui est la somme des DDL des nœuds qui le composent. Le nombre de nœuds est aussi associé à la rigidité intrinsèque de l'élément fini.
Les éléments finis peuvent être de 1er ordre ou d'ordre supérieur. Le premier ordre défini une arête uniquement par ses 2 points d'extrémité. L'arête ne peut avoir qu'une représentation linéaire. On parle alors d'éléments à interpolations linéaires
Le 2nd ordre (quadratique) lui, introduit un nœud intermédiaire sur chaque arête lui permettant ainsi des représentations curvilignes. Des solveurs spécifiques tels que IMPETUS AFEA permettent jusqu'à l'usage d'éléments d'ordre 4. Un article sera dédié sur l'ordre des éléments.

Noeuds dans les éléments finis dans ABAQUS
Formulation des éléments finis
Elle fait référence aux équations mathématiques qui décrivent le comportement de l'élément fini utilisé au regard du problème physique à résoudre. La formulation permet par exemple de tenir compte :
- De la matière : formulation Lagrangienne pour les structures et Eulérienne pour les fluides et matériaux hautement visqueux
- Des modes de déformations spécifiques aux familles d'éléments : Pour les éléments solides, on peut citer la formulation hydride (H) pour l'incompressibilité, incompatible (I) pour la flexion, modifié (M) pour optimisation du calcul des contraintes.
Pour les éléments shell, les formulations thin shell, thick shell permettent de traduire selon qu'on soit en hypothèse de contraintes planes ou de déformation plane.
Méthode d'intégration des éléments finis
Dans un élément fini, plusieurs champs ou quantités (contraintes, déformations,…) sont déterminées en se basant sur le calcul du volume de l'élément à un instant donné. Ce calcul est réalisé par le solveur en chaque point d'intégration en utilisant la méthode de quadrature de Gauss. Plus le nombre de points d'intégration est élevé, plus le temps de résolution l'est également, augmentant ainsi le coût du calcul.
ABAQUS dispose d'éléments finis avec une intégration dite réduite dans lesquels le nombre de points d'intégrations est moins important que les éléments de référence.

Intégration réduite dans les éléments finis ABAQUS
Conclusion
La méthode des éléments finis offre un large panel de possibilités pour la résolution de problèmes mécaniques en général.
Nous avons vu dans cet article les principaux points à considérer dans le choix d'un type d'éléments finis afin de trouver la meilleure solution : la plus précise et la moins couteuse.
Le prochain article sera consacré à l'interpolation dans les éléments et aux différences entre un maillage hexaédrique et tétraédrique (caractéristique du nombre de noeuds dans un élément fini).
Bibliographie
ABAQUS Documentation
Autres ressources
1. Jacques MAUREL. Unbalanced rotor behavior. Youtube channel
2. ONEPROD. Concepts of balancing: Types of Unbalance. Youtube channel
3. Grasp Engineering. Introduction to rotordynamic FE Analysis. Youtube channel
4. Rotor dynamics, Bearing, Motor. Rotor dynamics 101: Part 1 - Introduction. Youtube channel